How To Find The Base Of A Right Triangle

Area of Right Triangle

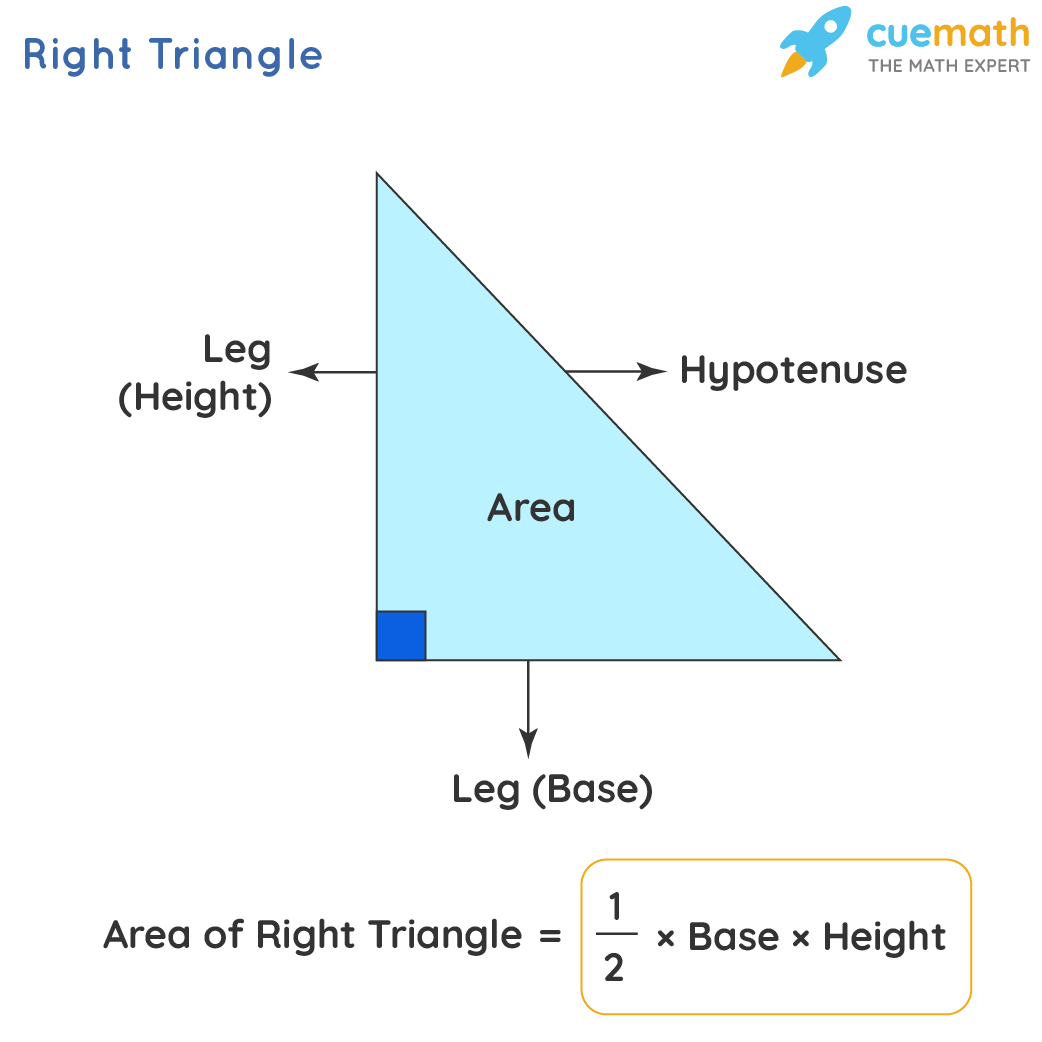
The expanse of a correct triangle is the portion that is covered inside the boundary of the triangle. A right-angled triangle is a triangle in which one of the angles is a right angle (90 degrees). It is just known as a right triangle. In a right-angled triangle, the side reverse to the right angle is chosen the hypotenuse and the other two sides are chosen legs. The 2 legs can be interchangeably called base and pinnacle. The area of right angle triangle formula is given in the image below.

ane.	What is Expanse of a Right Triangle?
2.	Area of Right Triangle Formula
3.	How to Derive Surface area of Right Triangle Formula?
iv.	Area of Right Triangle with Hypotenuse
five.	FAQs on Area of a Right Triangle

What is Area of a Right Triangle?

The area of a right-angled triangle, as we discussed before, is the infinite that is inside it. This infinite is divided into squares of unit length and the number of unit squares that are inside the right triangle is its area. The area is measured in square units. Let usa consider the post-obit right triangle whose base is iv units and summit is 3 units.

Can y'all endeavour counting the number of unit squares inside this triangle? In that location are half-dozen unit squares in total. And then the area of the above triangle is 6 square units. Only it is non possible to calculate the area of a right triangle always past counting the number of squares. At that place must be a formula to do this. Let us run across what is the formula for finding the surface area of a correct triangle.

Expanse of Right Triangle Formula

In the to a higher place case, if we multiply the base of operations and height, we get iii × 4 = 12 and if we divide information technology by 2, we get half-dozen. So the area of a correct triangle is obtained by multiplying its base and height and so making the production half.

Area of a right triangle = one/ii × base × height

Examples:

• The expanse of a right triangle with base 6 ft and peak four ft is 1/2 × half dozen × 4 = 12 ft².
• The area of a right triangle with base x thou and height five thou is 1/2 × ten × 5 = 25 m^two.
• The surface area of a right triangle with base 11 in and elevation 5 in is 1/two × 11 × v = 27.5 in^two.

How to Derive Area of Right Triangle Formula?

Consider a rectangle of length l and width westward. Also, draw a diagonal. You tin see that the rectangle is divided into two right triangles.

We know that the area of a rectangle is length × width. And then the area of the in a higher place rectangle is l × due west. We can see that the ii right triangles are coinciding as they can be arranged such that one overlaps the other. Thus, the area of the rectangle is equal to twice the expanse of one of the above right triangles. i.e.,

Expanse of rectangle = 50 × w = 2 × (Area of one right triangle)

This gives,

Area of 1 correct triangle = 1/2 × 50 × w.

Nosotros unremarkably correspond the legs of the right-angled triangle as base and height.

Thus, the formula for the area of a correct triangle is, Surface area of a right triangle = one/2 × base × height.

Area of Right Triangle With Hypotenuse

Let u.s.a. recollect the Pythagoras theorem which states that in a right-angled triangle, the square of the hypotenuse is the sum of the squares of the other 2 sides. i.e., (hypotenuse)² = (base)² + (height)ⁱⁱ.

Though it is not possible to find the surface area of a right triangle just with the hypotenuse, it is possible to find its area if we know i of the base and height along with the hypotenuse. Allow us see an instance.

Example: Find the area of a right bending triangle whose base is vi in and hypotenuse is 10 in.

Solution:

Substitute the given values in the Pythagoras theorem,

(hypotenuse)ⁱⁱ = (base of operations)² + (summit)²

10² = 6^two + (height)²

100 = 36 + (height)²

(height)² = 64

acme = √(64) = viii in.

Then, the surface area of the given triangle = 1/2 × base × height = 1/ii × 6 × viii = 24 inⁱⁱ.

Area of Right Triangle Examples

1. Example 1: The longest side of a bread slice that resembles a right triangle is thirteen units. If its superlative is 12 units, discover its area using the expanse of a right triangle formula.

   Solution:

   We know that the longest side of a right triangle is called the hypotenuse.

   And so, information technology is given that hypotenuse = 13 units and elevation = 12 units.

   Substitute the given values in the Pythagoras theorem,

   (hypotenuse)ⁱⁱ = (base)² + (height)²

   thirteen² = (base of operations)² + (12)²

   169 = (base)² + 144

   (base)ⁱⁱ = 25

   base of operations = √(25) = five units.

   The expanse of the staff of life slice = 1/2 × base × height = 1/two × v × 12 = 30 square units.

   Therefore, the area of the given breadstuff slice = 30 square units.

2. Example 2: A swimming pool is in the shape of a right triangle. Its sides are in the ratio 3:4:5. Its perimeter is 720 units. Find its area.

   Solution:

   Permit u.s.a. assume that the sides of the swimming pool exist 3x, 4x, and 5x.

   It is given that its perimeter = 720 units.

   3x + 4x + 5x = 720

   12x = 720

   ten = sixty

   Then the sides of the triangle are,

   3x = 3(threescore) = 180 units

   4x = 4(60) = 240 units

   5x = 5(60) = 300 units

   Since 300 units is the longest side of the swimming pool (which is in the shape of a right triangle), it is the hypotenuse.

   So, 180 units and 240 units must exist the base and the height of the swimming pool interchangeably.

   Using the area of right triangle formula,

   The surface area of the swimming pool = 1/2 × base × height = 1/2 × 180 × 240 = 21,600 unitsⁱⁱ.

   Therefore, the expanse of the given swimming pool = 21,600 units².

go to slidego to slide

Breakdown tough concepts through simple visuals.

Math will no longer be a tough subject, especially when you empathise the concepts through visualizations.

Volume a Free Trial Class

Practice Questions on Area of Right Triangle

get to slidego to slide

FAQs on Area of Correct Triangle

What is the Area of a Right Triangle?

The area of a right triangle is defined as the total infinite or region covered by a correct-angled triangle. It is expressed in square units. Some mutual units used to correspond area are mⁱⁱ, cm², in², yd², etc.

What is the Formula for Finding the Area of a Correct Triangle?

The surface area of a correct triangle of base b and pinnacle h is ane/2 × base of operations × height (or) 1/2 × b × h square units.

How Do You Notice the Perimeter and Area of a Correct Triangle?

The surface area of a right triangle of base b and peak h is found using the formula 1/two × b × h and its perimeter is obtained by just calculation all the sides. In case only ii of its sides are given, then we use the Pythagoras theorem to discover the third side.

How Do Y'all Find the Area of a Correct Triangle Without the Base?

If simply the tiptop and hypotenuse of a right triangle are given, then before finding the area of the triangle, we showtime need to detect the base using the Pythagoras theorem. Then we can employ the formula 1/2 × base × height to find its expanse. For instance, to detect the area of a correct triangle with a summit of four cm and hypotenuse 5 cm, we first find its base using the Pythagoras theorem. Then we get,

base = √[(hypotenuse)² - (height)²] = √(5² - four^two) = √9 = 3 cm.

Area of the right triangle = 1/2 × 3 × four = 6 cm^two.

How Do You Observe the Expanse of a Right Triangle Without the Height?

If only the base of operations and hypotenuse of a right triangle are given, then earlier finding the expanse of the triangle, nosotros first need to find the height using the Pythagoras theorem. And so we tin can employ the formula 1/2 × base x height to discover its area.

For instance, to notice the area of a correct triangle with a base of operations of 4 cm and hypotenuse 5 cm, nosotros outset observe its summit using the Pythagoras theorem. Then we become

height = √[(hypotenuse)² - (base of operations)²] = √(5² - ivⁱⁱ) = √nine = 3 cm.

Area of the triangle = 1/2 × 3 × 4 = 6 cm².

How Exercise You Find the Area of a Right Triangle With a Hypotenuse?

In fact, it is not possible to find the area of a right triangle only with the hypotenuse. We demand to know at least one of the base and height along with the hypotenuse to notice the surface area.

• If we know the base of operations and the hypotenuse, nosotros discover the height using the Pythagoras theorem.
• If we know the height and the hypotenuse, we find the base using the Pythagoras theorem.

Then, we tin can find the area of the right triangle using the formula 1/2 × base × height.

Source: https://www.cuemath.com/measurement/area-of-right-triangle/

Posted by: myersseencephe.blogspot.com

Share this post